吉川 耕司 准教授
宇宙物理研究部門
宇宙にはダークマターやバリオン(原子から構成される物質)などからなる様々な粒子が広がっています。粒子の密度が高いところもあれば低いところもあり、その分布の成り立ちを知るためには計算機を用いたシミュレーションが不可欠です。吉川先生は、これまで解くことが難しかった問題の高精度な計算手法を開発し、宇宙の成り立ちに迫る研究を進めています。
(2021.12.24 公開)
宇宙の謎を解く鍵 −ブラソフ方程式−
宇宙には、銀河やガスが多く集まる領域やそれらがほとんど存在しない領域があり、その分布は均質ではありません。このような宇宙全体の非一様な構造のことを「宇宙大規模構造」と呼びます。宇宙大規模構造の形成には、宇宙に大量に存在するダークマターやニュートリノが関わっていると考えられています。現在のような宇宙大規模構造がどのようにできたのかを知るためには、宇宙の初期にほぼ一様に分布していたダークマターやニュートリノの分布が、時間と共にどのように変化したのかを知ることが手がかりになります。
これまで、ダークマターやニュートリノの運動のシミュレーションには、ある程度の粒子の集団を一つの粒子(超粒子)とみなして計算するN体シミュレーションという手法が使われてきました。しかしこの手法には、連続で滑らかな粒子の分布を大きい超粒子の分布で置き換えて表現するため、計算結果にノイズが入るという欠点がありました。
粒子の動き(運動)は、粒子の位置と速度で表されます。粒子は、位置と速度の両方の情報を含む位相空間(図1)の中を、時間の経過とともに連続的に移動します。このような粒子の集団的な動きを表す方程式が、ブラソフ方程式(図2)です。数値シミュレーションを使ってブラソフ方程式を解くことができれば、粒子の運動を第一原理的1)にシミュレーションすることができます。しかし、これまでこの計算はほとんど挑戦されてきませんでした。

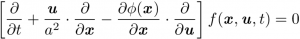
分割数を増やさずに精度を上げる
宇宙の研究では、計算領域を小さく分割して数値シミュレーションを行います。通常の3次元空間(実空間)を扱う場合、x軸、y軸、z軸の辺をそれぞれN個に分割すると、Nの3乗に比例するメモリ量が必要になります。一方、ブラソフシミュレーションは空間3次元に速度空間3次元を加えた6次元の位相空間を扱うため、各辺をN個に分割した場合にNの6乗に比例するメモリ量が必要になってしまいます。精度を上げるには分割数を増やす必要がありますが、ブラソフシミュレーションの場合は分割数を増やすとメモリ量が膨大となってしまい、スーパーコンピュータでも実用的な計算ができないという点が大きな壁となっていました。
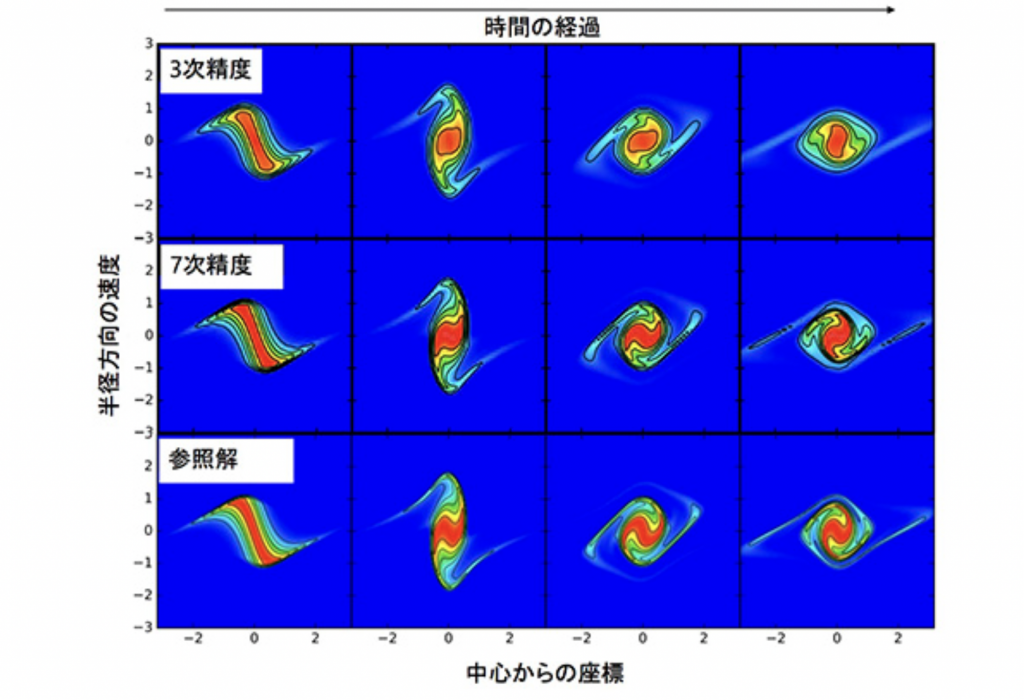
そこで、吉川先生はブラソフ方程式の数値拡散という性質に着目しました。空間を分割してブラソフ方程式を解くと、位相空間での粒子の密度を示す分布関数の輪郭が時間経過とともにぼやけてしまうという性質があります(図3)。これを数値拡散と呼びます。これは計算過程で行う近似によって生じるもので、なくすことができません。吉川先生はこの近似の精度を上げることで、数値拡散を減らし、ブラソフシミュレーションの精度を上げる手法を開発しました。
この手法を使うことで、分割数を増やさずにブラソフシミュレーションの精度を上げることができ、結果として同じメモリ量でこれまでのブラソフシミュレーションよりも格段に精度の高い結果を得ることが可能になりました。
さらに、スーパーコンピュータの性能向上も合わさり、世界有数の高性能なスーパーコンピュータ「京」や「富岳」、Oakforest-PACSを使うことで、世界で初めてブラソフシミュレーションを実用化することに成功しています(図4)。「富岳」を用いた成果は、スーパーコンピュータを用いた科学・技術分野の研究の中で、その年に最も顕著な成果を挙げた研究グループに贈られる米国計算機学会のゴードン・ベル賞の2021年最終候補(ファイナリスト)に選出されました。
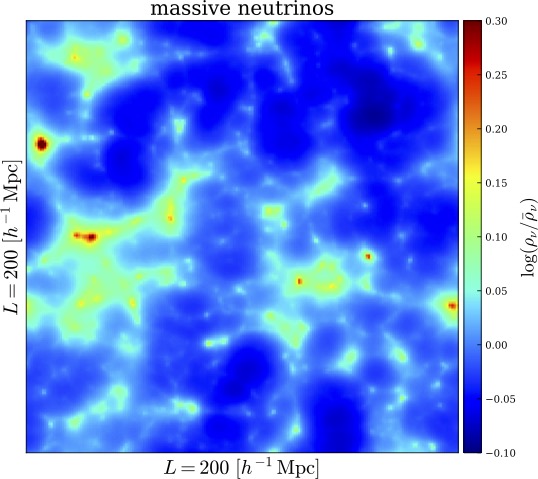
宇宙は広く、ダークマターやニュートリノも場所によって様々な密度分布をしていると考えられています。今後も様々な条件の場所を標的にブラソフシミュレーションを解いていくことで、宇宙の進化の謎に迫ることができます。また、ブラソフシミュレーションはプラズマの研究への応用も期待されています。
【用語】
1)第一原理計算:実験で得られた数値や経験によるパラメータを使わず、物理の基本法則(第一原理)に基づいた計算を行う手法。
さらに詳しく知りたい人へ
- 「富岳」を用いた宇宙ニュートリノの数値シミュレーションに成功〜2021年ゴードン・ベル賞ファイナリストに選出〜」(2021年10月28日プレスリリース)
- 「宇宙を飛び交うニュートリノの動きを明らかに〜世界初の6次元シミュレーションに成功〜」(2020年12月1日プレスリリース)
- 「ニュートリノや宇宙プラズマのシミュレーション精度が飛躍的に向上 –ブラソフ方程式の高精度数値解法を開発」(2017年11月13日プレスリリース)
- 宇宙空間に広がる素粒子の運動を探る – ブラソフ方程式の高精度シミュレーション(academist Journal, 2018.1.4)

