清水則孝　准教授

原子核物理研究部門

清水先生は原子の中心にある原子核の性質を調べるため、コンピューターを用いた数値計算による理論研究をされています。

特に、清水先生は殻模型計算と呼ばれる手法を用いて原子核の構造を明らかにしています。

(2024.5.29 公開)

「魔法の数」から生まれた殻模型計算

原子の中の電子は2,8,18,32…個のときに安定するという性質があります。これらの個数の電子が入る電子殻をそれぞれK殻,L殻,M殻…と呼びます。同じような殻構造は原子の中心にある原子核でもみられ、原子核の場合は陽子や中性子（総称して核子）が各々2,8,20,28,50,82,…個のときに安定する性質があります。そして原子核が安定になる核子の数を「魔法数」（図1）と呼び、魔法数と魔法数の間に核子が入ることのできる「副殻」がいくつかあります。

 

 

 

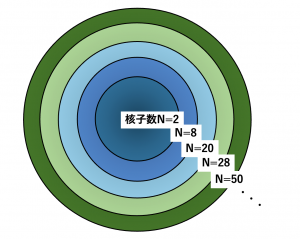
原子核が殻構造をもつという性質に基づいて考えだされたのが、殻模型という理論モデルです。殻模型では考えたい核子数より内側の魔法数以下の核子をある質量を持つコアとみなし、魔法数以上の核子のみをバラバラの粒子として扱います。

また、原子核はとても小さい核子が集まってできているので、その性質を調べるためにはたくさんの粒子に関する量子力学的な式を解く必要があります。この量子力学的な式をシュレーディンガー方程式といい、「ハミルトニアン」と「波動関数」,「エネルギー（質量）」から構成されています（図2）。ハミルトニアン（注1）は粒子が存在する環境を説明する役割、波動関数はその環境下での粒子の状態を説明する役割を持っています。殻模型計算ではハミルトニアンを設定してシュレーディンガー方程式を解くことで波動関数とエネルギーを得ます。正しいハミルトニアンを用いてこれらの解が得られれば、原子核の構造が分かる、ということになります。

 

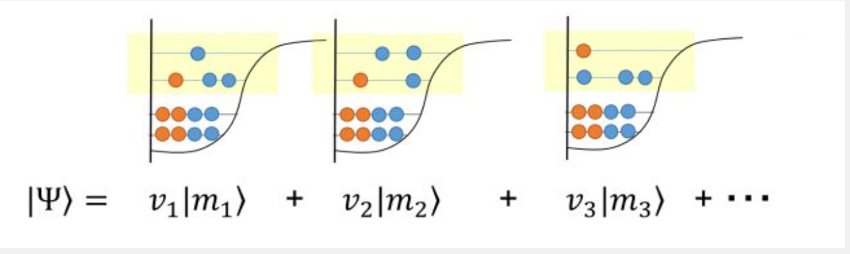
さらに、波動関数は「基底」と呼ばれる関数の足し算でできている関数で、この基底の大まかな形は自分で設定してから方程式を解くという手順になっています。殻模型計算では図3のように、「それぞれの副殻に核子がどう詰まっているか」という組み合わせのパターンを基底とし、これらの基底を全て足し算したものを波動関数として設定しています。

原子核は球形のものもあれば、みかん型やレモン型のように変形しているものも存在します。さらに球形でもあり変形もしている、という両方の性質を持った不思議な原子核も存在するのですが、殻模型計算はこのような原子核の性質を表現することを得意としています。

 

原子核の構造を決定するために解くシュレーディンガー方程式は、行列の方程式におきなおして解くことができ、組み合わせのパターンの数がその行列の次元に相当します（多田野先生の記事参照）。核子数が増えていくとパターンの数が組み合わせ爆発的に増えるため、直接解こうとするととても計算時間がかかり、現在のスーパーコンピュータでも計算しきれないといった問題が起きてしまいます。さらに、大きく変形している原子核では、コアをこわすような基底も新たに考える必要があり、これまでの殻模型計算では不可能でした。

 

仮想の粒子「準粒子」が大活躍

そこで、清水先生は基底を設定する際に使う関数の形を工夫することで、計算量の削減と球形・変形両方の性質を持つ原子核の再現に成功しました。

先ほど、基底は「核子が副殻に詰まるパターン」を使うと言いましたが、清水先生はこれを「準粒子が副殻に詰まるパターン」に変更しました。「核子」を「準粒子」に変更したのです。準粒子というのは、計算する上で用いる仮想の粒子です。通常、私たちは粒子が「存在する」または「存在しない」のどちらかであると考えますが、準粒子の場合は「この核子は○%存在する」というように存在する確率を決めることができます。準粒子という仮想の粒子を基準にして波動関数を設定すると、核子を基準にするよりも数値計算上で求めたい解により早く辿り着くことができます。

この清水先生の計算手法を用いると、150Nd（ネオジム150）原子核は、小さめの変形と、大きな変形の二つの「形」がいりまじっているような珍しい原子核であることがわかってきました。この原子核は2重ベータ崩壊（注2）という特別な崩壊をおこすので、ニュートリノの質量を調べる実験に使われています（日野原先生の記事参照）。その実験に必要な情報を提供することにもつながりました。

 

原子核の構造を調べる計算方法は殻模型計算の他にも第一原理計算や密度汎関数法などがあります。清水先生は今後、これらの計算方法を繋ぐ研究がしたいと考えています。これら3つの計算方法にはそれぞれに良いところがあるので、これらを掛け合わせた方法ができたら、今まで発見されていなかった驚くべき原子核の性質が見えてくるかもしれません。

 

　　　　　　　　　　　　　　　　　　　　　　　　　　　（文・広報サポーター　類家千怜）

 

 

 

用語

（注1）ハミルトニアン：考えている系全体のエネルギーを表す関数

（注2）2重ベータ崩壊：中性子が陽子に変わるベータ崩壊が同時に2回起きる現象。

 

さらに詳しく知りたい人へ

殻模型の可能性を広げるKSHELL-原子核の未知に挑む大規模計算